Teorema de Pitágoras
¿Qué es?
Es una propiedad descubierta por el matemático griego llamado Pitágoras “de ahí el nombre del teorema”, que establece que la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa del triangulo rectángulo.
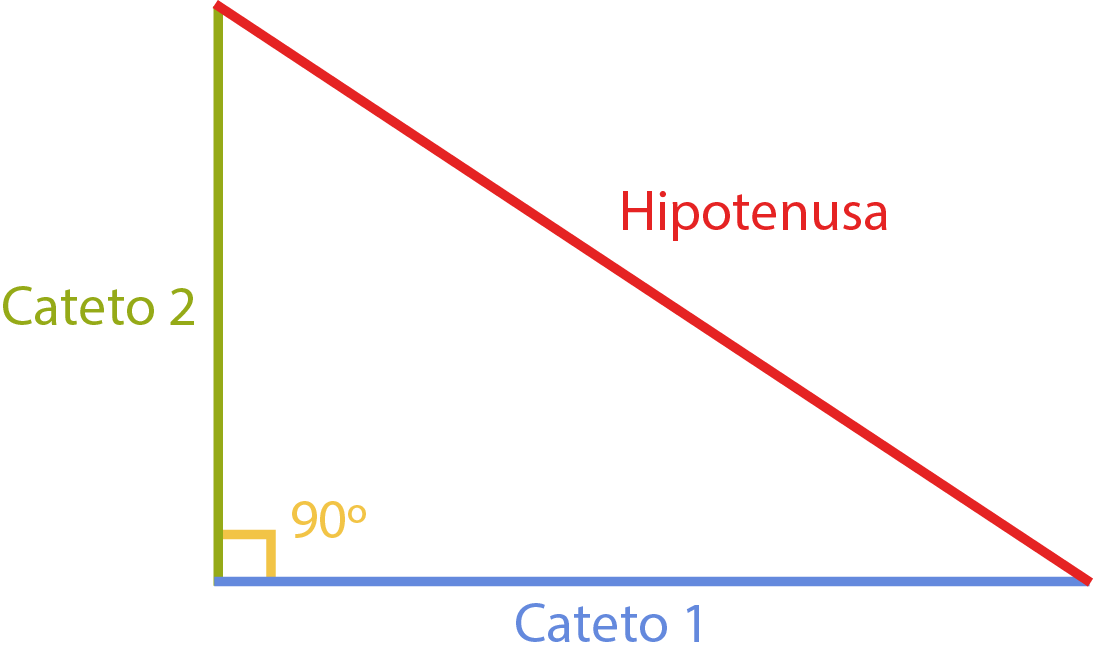
¿Qué es un triangulo rectángulo?
El triangulo rectángulo es un polígono de 3 lados y uno de sus ángulos es recto es decir de 90 grados; además sus ángulos menores deben sumar 90 grados. Sus partes son: tiene un lado de mayor longitud llamado “Hipotenusa” y otros dos llamados “catetos, uno de esos es el cateto opuesto el cual está al frente del ángulo y el otro es el cateto adyacente que es el que está pegado al ángulo.
Tipos de triángulos rectángulos
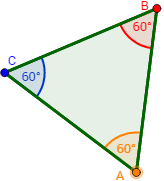
*Equilátero:
- Los 3 lados (a,b y c) son iguales
- Los 3 ángulos interiores son iguales
*Escaleno:
-Los 3 lados son distintos
-Los 3 ángulos son también distintos
*Isósceles:
-Tiene 2 lados iguales (a y b) y un lado distinto (c)
-Los angulos (a y b) son iguales y el otro angulo (c) es distinto
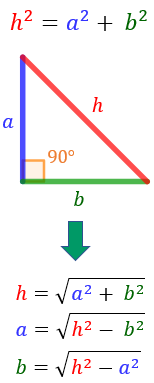
Formula del teorema de Pitágoras
Su fórmula es:
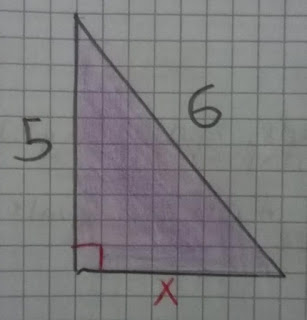
Proceso del teorema de Pitágoras
Teniendo en cuenta la formula empezamos a reemplazar los datos:
h2 = c2 + c2
62 = 52 + c2
62 - 52 = c2
36-25 = c2
11 = c2
√11 = c
3,316 = c
Comprobar el resultado
Una de las maneras más fáciles de comprobar si el resultado está bien, es teniendo en claro que la longitud de los catetos no puede ser mayor a la longitud de la hipotenusa
Ejercicios
-N.1
Juan se sitúa a 10 m de distancia de un rascacielos, el patea un balón el cual rompe un vidrio del edificio que esta a una altura de 5 m. ¿Qué distancia recorre el balón que pateo Juan y se estrella en la ventana?
h2 = c2 + c2
h2 = 102 + 52
h2 = 100 + 25
h2 = 125
h = √125
h = 11,18 m
R/: El balon que pateo juan y que se estrello en la ventana del edificio recorre una distancia de 11,18 m.
-N.2
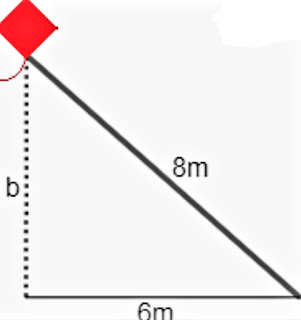
¿A que altura esta la cometa de isabella, si su cuerda mide 8 metros y tendria que moverse 6 metros para situarse debajo de ella?
h2 = c2 + c2
82 = C2 + 62
82 - 62 = C2
64 - 36 = C2
28 = C2
√28 = C
5,2915 m = C
R/: La cometa de isabella esta a una altura de 5,2915 m.
Relatividad del movimiento
Ejemplo:
1. ¿Cuál es el desplazamiento de un móvil que está situado en dos instantes distintos en X1 = 10m y X2 = -20m?
R/: El desplazamiento del móvil es de -20m.
Coordenadas de posición en el plano
Un vector es un segmento de recta, a partir de un punto en el espacio y representa una magnitud “todo aquello que se pueda medir”. Las coordenadas de un punto es un par ordenado (x,y) .
Formula de la distancia: r = √x2+ y2
Ejemplo
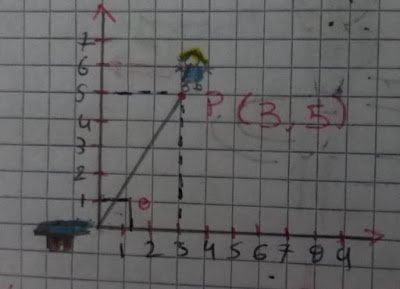
Pilar está en la posición r= (3m)i + (5m)j, respecto a su casa encontramos a que distancia se halla pilar de donde vive.
-Distancia:
r = √x2+ y2
r = √32 + 52
r = √9 + 25
r = √34
r = 5,8330 m
R/: pilar se halla a 5,8330 m de distancia de la casa donde vive.
Funciones Trigonometría
Son las funciones de un ángulo. Estas usualmente incluyen términos que describen la medición de ángulos y triángulos, tal como seno, coseno, tangente, cotangente, secante y cosecante.
1. Seno
* Contraria del seno es Cosecante
* Contraria del coseno es Secante
3. Tangente
* Contraria del tangente es Cotangente
Ejercicio:
Calcula todas las razones trigonométricas de los ángulos del triángulo.
h2 = c2 + c2
112 = 72 + c2
112 - 72 = C2
121 - 49 = C2
72 = C2
√72 = C2
8,48 = C2
*Razones Trigonométricas de θ
*Razones trigonométricas de














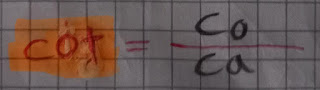



Comentarios
Publicar un comentario